Analisi CFD
-------------------------
Analisi FEM
-------------------------
Vantaggi FEM/CFD
-------------------------
Cinematica

Le equazioni sulle quali si fonda la fluidodinamica computazione C.F.D. sono le equazioni di Navier-Stokes:

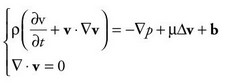
Che in formulazione estesa possono essere scritte come:

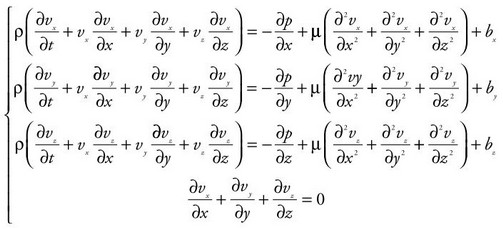
Sono 4 equazioni scalari con 4 incognite la cui principale difficoltà di risoluzione risiede nel termine non lineare

considerato una delle fonti più forti sorgenti di non linearità presenti nella fisica.

Non esistono soluzioni analitiche (ovvero formule)  a queste equazioni, tranne che in rari casi. Inoltre la risoluzione numerica delle equazioni di Navier Stokes per flussi turbolenti è concettualmente possibile ma attualmente impraticabile.

Per questa difficoltà, vengono utilizzate le equazioni Navier-Stokes in forma di Reynolds (formulazione RANS - Reynolds-averaged Navier-Stokes) in cui si hanno le medesime grandezze ma si semplifica il sistema ricercando la soluzione media nel tempo.
Tale semplificazione comporta un'indeterminzione del problema: ci sono 4 equazioni e 10 incognite.

Poiché è necessario, per calcolare il moto medio, considerare gli effetti della turbolenza (tali effetti sono rappresentati dagli sforzi di Reynolds) si devono introdurre dei metodi aggiuntivi per chiudere il modello. Da qui nascono i vari modelli di turbolenza che sono presenti nel panorama CFD odierno come:

- il modello di turbolenza k-epsilon

Un approccio diverso al sistema RANS è rappresentato dalla formulazione LES (Large Eddy Simulation).

Nei fenomeni di turbolenza, le strutture vorticose più grandi trasferiscono energia verso strutture vorticose sempre più piccole con una schema a cascata. Sono le turbolenze minori a dissipare energia. Il modello LES risolve le equazioni di Navier-Stokes (direct numerical simulation DNS) per le strutture vorticose maggiori e modellizza quelle minori.
Per questo motivo, LES tende ad essere più preciso di RANS.