Mesh del Dominio di Calcolo a Elementi Finiti FEM
SIMULAZIONI > TEORIA FEM
Analisi CFD
-------------------------
Analisi FEM
MESH - METODO A ELEMENTI FINITI
L'Analisi agli Elementi Finiti (Analisi FEM) è un potente metodo numerico per risolvere problemi ingegneristici complessi, come la determinazione di tensioni, deformazioni, flusso di calore o campi elettromagnetici in un oggetto. Il cuore di questo metodo risiede in un'operazione fondamentale: la discretizzazione. E la mesh è lo strumento con cui questa operazione viene realizzata.
Cos'è la Mesh nel metodo a elementi finiti?
Per poter applicare il metodo a elementi finiti, una passaggio fondamentale è la frammentazione (discretizzazione) del dominio di calcolo. Si passa da un modello geometrico continuo (rappresentazione reale) ad un modello geometrico discretizzato (rappresentazione approssimata) e si risolvono, per via numerica, le equazioni che descrivono il modello fisico-matematico.
Il principio ingegneristico, sul quale il metodo a elementi finiti si basa, è quello del "divide et impera". Un problema complesso può essere scomposto in tanti problemi semplici. La soluzione di tutti i sottoproblemi porta alla soluzione del problema generale.
In altre parole, si passa da un numero di gradi di libertà infinito, il continuo, ad un numero di gradi di libertà finito, la mesh.
Un esempio di mesh (discretizzazione) del dominio di calcolo è il seguente:
Caratteristiche della Mesh: da cosa è formata una Mesh?
La mesh o griglia è composta da geometrie primitive (elementi) di forma matematicamente definita.
Sono principalmente triangoli e quadrilateri per domini 2D
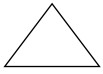
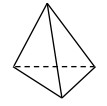
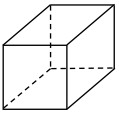
esaedri e tetraedri per domini 3D
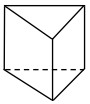
oppure, in casi meno frequenti, cuneiformi oppure poliedrici
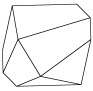
Le parti da cui è composto un elemento finito sono i nodi (vertici), gli spigoli (edge) e le facce (face).
Negli ultimi anni sono stati introdotti elementi che, a parità di topologia, hanno un numero maggiore di nodi.
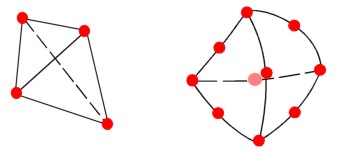
La possibilità di avere un maggior numero di nodi per spigolo permette, tra i principali vantaggi, elementi che meglio si adattano a geometrie curvilinee. Per esempio, è necessaria una minor quantità di elementi per poter approssimare superfici cilindriche come i fori. Ciò si traduce in un guadagno nei tempi di calcolo e una descrizione più precisa della geometria in esame.
Perché è Così Critica? Il Compito della Mesh
La mesh non è un semplice reticolo; è l'infrastruttura su
cui poggia l'intera simulazione. I suoi compiti sono cruciali:
- Approssimazione Geometrica: Più fitta è la mesh, migliore sarà l'approssimazione della geometria reale, specialmente in zone curve o con dettagli complessi.
- Base per le Equazioni: Il sistema di equazioni globali, che risolve il problema fisico, viene assemblato e risolto sui nodi della mesh. L'analisi avviene sulla mesh, non sull'oggetto originale.
- Propagazione dell'Informazione: Le sollecitazioni e le deformazioni si trasmettono da un elemento all'altro attraverso i nodi comuni, simulando il comportamento continuo del materiale.
Tipi di Mesh e Strategie di Discretizzazione
Esistono diverse filosofie per generare una mesh, ognuna con i suoi pro e contro:
- Mesh Strutturata (Mappata): Gli elementi sono disposti in file e colonne ordinate, formando una griglia regolare. È molto efficiente ma applicabile solo a geometrie semplici e regolari.
- Mesh Non Strutturata: Gli elementi sono disposti in modo irregolare, il che permette di adattarsi a geometrie estremamente complesse. La maggior parte dei software moderni utilizza questo tipo, spesso basato su triangoli in 2D e tetraedri in 3D.
- Mesh Ibrida: Combina mesh strutturate in aree regolari e non strutturate in zone complesse, per ottimizzare accuratezza e tempi di calcolo.
L'Arte di "Meshare": Bilanciare Accuratezza e Costo Computazionale
Creare una buona mesh è un'operazione che richiede esperienza e bilanciamento. Due concetti chiave sono:
Convergenza della Mesh: Un risultato è affidabile solo quando, affinando progressivamente la mesh (aumentando il numero di elementi), la soluzione (es. la tensione massima) non cambia in modo significativo. Questo processo è essenziale per validare i risultati.
Affinamento Adattativo (Mesh Refinement): Per ottimizzare le risorse, si utilizza una mesh più fitta solo dove serve, tipicamente in zone di gradiente elevato (dove le grandezze fisiche cambiano rapidamente, come intorno a fori, intagliagli o spigoli vivi). Le aree dove le sollecitazioni sono basse possono avere una mesh più rada.
Mesh: Sintesi
La mesh è il ponte indispensabile tra il mondo fisico continuo e il modello matematico discreto dell'Analisi FEM. È lo "scheletro computazionale" sul quale l'analisi prende vita. Una mesh ben costruita non è solo un reticolo che ricopre una geometria; è una rappresentazione intelligente e efficiente del dominio fisico, che permette di svelare, numero dopo numero, il comportamento nascosto della materia sotto l'azione delle forze.
Per ulteriori informazioni su come implementare con successo l'Analisi FEM nei tuoi progetti o per avere Consulenza sulle Analisi FEM, contattaci!